Copyright License Agreement

Presentation of the articles in the Topics in Middle Eastern and North African Economies was made possible by a limited license granted to Loyola University Chicago and Middle East Economics Association from the authors who have retained all copyrights in the articles. The articles in this volume shall be cited as follows: Erlat, H., N. Ozdemir, “A Panel Approach to Investigating the Persistence in Turkish Real Exchange Rates”, Topics in Middle Eastern and North African Economies, electronic journal, Volume 5, Middle East Economic Association and Loyola University Chicago, September, 2003. http://www.luc.edu/publications/academic/

A PANEL APPROACH TO INVESTIGATING THE PERSISTENCE IN TURKISH REAL EXCHANGE RATES

Haluk Erlat

Middle East Technical University

Email: herlat@metu.edu.tr

Nilufer Ozdemir

Central Bank of Turkey

Email: Ozdemir@tcmb.gov.tr

JEL Classification: F31, F41, C22, C23

Key Words: Real Exchange Rates, Purchasing Power Parity, Panel Unit Root Testing

Abstract: Unit root tests have been applied to Turkish real exchange rates to test the absolute version of the purchasing power parity (PPP) hypothesis. A survey of the evidence regarding the PPP hypothesis for Turkey, as given in Erlat (2003), indicates that it does not favour the PPP hypothesis. This evidence is based, to a great extend, on the Augmented Dickey-Fuller (ADF) test which known to have very low power. One of the alternatives suggested to deal with this problem is to implement panel unit root tests. This is what we set out to do in this paper and find, particularly when we take into account the dependence between the series, that we are still not able to find support for the PPP hypothesis in the case of Turkey.

1. Introduction

Testing whether real exchange rates are stationary and, thereby, obtaining evidence on the absolute version of the purchasing power parity (PPP) hypothesis has, initially, been done by using the Augmented Dickey-Fuller (ADF) statistic to test for a unit root. Subsequently, to mitigate the low power of the ADF test, several alternatives have been used for the same purpose.. Panel unit root testing is one of these alternatives.

The logic behind the use of a panel unit root test is to combine the information from time series with the information from cross-sectional units. The addition of cross-sectional variation to time series variation improves estimation efficiency, leading to smaller standard errors and, consequently, to higher t-ratios. Levin, Lin and Chu (LLC) (2002) show that, in situations where there is not enough time-series variation to produce good power in the ADF test, a relatively small amount of cross-section variation can result in substantial improvement.

Unit root tests have been applied to Turkish real exchange rates to test the absolute version of the PPP hypothesis. Erlat (2003) contains a survey of all (both unit root and cointegration based) evidence regarding the PPP hypothesis for Turkey. The results, usually, do not favour the PPP hypothesis, except when nonlinear time series methods are used as in Sarno (2000). Erlat (2003) maintains that Sarno’s findings may be accounted for by using linear methods with multiple shifts in the deterministic terms taken into account, and by using fractional integration techniques with structural shifts. His application of these models to the two primary bilateral Turkish real exchange rates; the $US and the German DM based rates, indicate that these two rates may, in fact, be taken to be stationary with significant long-memory components. These findings may not provide evidence in favour of the absolute PPP hypothesis in its purest form (where there is no trend term or structural shifts) but they do indicate that the absolute version of the “quasi” PPP hypothesis cannot be rejected for Turkey.

In this paper, we utilize panel procedures to see if they give us evidence in favour of the PPP hypothesis, not its “quasi” version; hence, structural shifts in the deterministic terms have not been taken into account in the present application. Panel procedures were first used on Turkish data by Ozdemir (2002), on which this paper is partially based. As we shall discuss below, the existing panel procedures, LLC (2002), Im, Pesaran and Shin (2000) and Hadri (2000), are, in general, based on the assumption that the series that make up the panel are independent of each other, which, of course, is hardly a realistic assumption to make where exchange rates are concerned. A common way to deal with this problem has been to subtract the means obtained for each time point across cross-sections, from the observations. An alternative, due to Taylor and Sarno (1998) and Breuer, McNown and Wallace (2001), handles the problem of dependence by considering the autoregressions corresponding to each series as a set of seemingly unrelated regressions. Taylor and Sarno consider a joint test of a unit root while Breuer et al. consider individual test, thereby complementing each other.

Ozdemir (2002) contains the results of applying these procedures to a panel of seventeen monthly Turkish real exchange rates that cover the period 1984.01-2001.06. In this paper we, in addition, implement a new procedure to account for the dependence between the series due to Bai and Ng (2001a and b). The idea underlying this procedure is to decompose the panel to its common and idiosyncratic components and apply tests of unit roots to these components separately. One can then apply the standard panel unit root tests to the idiosyncratic components since they will now be asymptotically independent.

Thus, the plan of the paper will be as follows: In the next section we shall give an account of the panel procedures utilized. Subsequently, in Section 3 we shall describe our data and, in Section 4, present the empirical results. The final section will contain our conclusions.

2. Panel Unit Root Tests

2.1. The Standard Procedures

We shall be interested in testing the presence of a unit root in a panel of real exchange rates, the natural log of which we shall denote by q_it and define as where e_it denotes the logarithm of the nominal exchange rate of Turkey with its ith trading partner (expressed as TL/Foreign Currency), p_it^*, the logarithm of the ith trading partner’s price level and p_t, the log of the domestic price level. We shall discuss the LLC, IPS and Hadri approaches to this problem.

For the LLC and IPS approaches, we shall start by considering the autoregressions used to obtain the ADF test for each time series in the panel. Let there be N such series. Then,

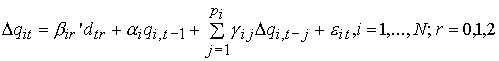(1)

where d_t0 = 0 or d_t1 = 1 or d_t2 = (1, t)’. Note that we allow for different configurations of the deterministic term and different lag lengths for each series. The choice of each p_i may be done by using a general-to-specific procedure based on either information criteria, such as AIC or the Schwartz criterion, or on sequentially testing the last coefficient of the .

In the LLC approach, it is assumed that, as opposed to the formulation in (1), all the a_i have a common value, a, so that the null hypothesis to be tested is

H₀: a = 0 vs. H₁: a < 0.

Thus, an estimator of a is obtained by controlling for the heteroscadasticity across the time series that make up the panel. The unit root test statistic is simply the t-ratio of a, adjusted in such a way that it is asymptotically normal under the null hypothesis.

The starting point of the IPS approach is also the ADF regressions given in (1). But, the null and alternative hypotheses are different from that of the LLC approach, where the rejection of the null hypothesis implies that all the series are stationary. We now have

H₀: a₁ = a₂ = … = a_N = 0 vs. H₁: Some but not necessarily all a_i < 0

The test statistic itself is rather simple to compute. Again, after deciding upon d_tr and the p_i, we obtain the t-ratios for the a_i, 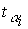, and calculate their arithmetic average, 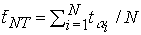. IPS show that 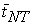may be adjusted to yield an asymptotic N(0, 1) statistic under the null hypothesis;

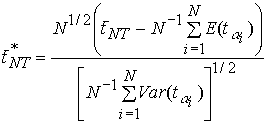
The and have been obtained by simulation and are given in Table 1 of IPS.

Finally, in the case of the Hadri approach, the null hypothesis is the stationarity of the series instead of nonstationarity. The framework is the one dealt with in Kwiatowski et al. (KPSS) (1992) for a single series. The models may now be expressed as,

(2)

where b_irt = b_i1t when r = 1 and b_irt = (b_i1t, b_i)’ when r = 2. We assume that the intercept, b_i1t, is generated by a random walk, , where E(u_it) = 0 and . In other words, we assume that the variances of the u_it are the same for every series. Thus, the hypothesis to be tested becomes,

H₀: vs. H₁:

However, we may assume that E(e_it) = 0 and ; i.e., that the variances of the e_it may not be the same for every series. We may also account for the fact that the e_it may be autocorrelated by considering the long-run variances of the e_it and estimate them as

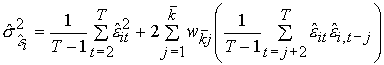(3)

where the are weights used to ensure that the are always positive. In our applications, we use the Bartlett weights, which may be expressed as .The resultant statistic to test H₀ would, then, simply be the average of the individual KPSS statistics for each series. Hadri shows that this statistic, appropriately standardized, will be asymptotically N(0,1) under the null hypothesis.

2.2 Dealing with the Problem of Dependence

The problem of dependence between the series that make-up the panel has several implications: (i) As O’Connell (1998) showed, panel unit root tests will overreject the null hypothesis of a unit root; there will be an upward bias in the size of the tests, giving the impression of high power. Such distortions in size will come about, particularly, if the dependence is due to cross-unit cointegration (Banerjee, Marcellino and Osbat, 2001). (ii) If the unit root null were not rejected, this would imply that there exists N independent unit roots. But, if these series have common stochastic trends, the number of unit roots would be less than N (Bai and Ng, 2001b). The procedures we are going to discuss in this subsection are designed to remove this dependence so that most, if not all, of these implications no longer hold.

The first solution to deal with the problem of dependence was implemented by LLC and IPS. They assume that, in addition to a series specific intercept and/or trend term as given in (1), there is a time specific intercept that may be estimated by taking the average across the series at each point in time. In other words, this dependence is accounted for by calculating , and subtracting it from each cross-sectional observation at point t; namely, for each t, using instead of q_it in the calculations given above. This correction will not remove the correlation between the series, but, as Luintel (2001) demonstrates, it may reduce it considerably.

The second solution would be to assume, at the outset, that the e_it of (1) are contemporaneously correlated so that the N equations involved may be treated as a set of seemingly unrelated regressions (SUR). Such an approach is taken by Taylor and Sarno (1998), Groen (2000) and Breuer, McNown and Wallace (2001).¹ The first two consider testing the joint null hypothesis

H₀: a₁ = a₂ = … = a_N = 0

while Breuer et al. (2001) test the individual hypotheses

H_0i a_i= 0, i = 1,...,N

Taylor and Sarno (1998) use the two-step Estimated GLS (EGLS) procedure to estimate the system of equations in (1) and test the joint null hypothesis using the Wald statistic, which they call the Multivariate ADF (MADF) statistic. Groen (2000), on the other hand, estimates the system by maximum likelihood and uses the likelihood ratio statistic to test the same hypothesis. We preferred to implement Taylor and Sarno (1998)’s approach since it is also the one taken by Breuer et al. (2001).

Now, Breuer et al. (2001) also estimate the same equations as in (1) but use the individual significance tests for the a_i. They call the corresponding t-ratios, the SURADF statistics. These may be regarded as complements to the MADF test as they would indicate which series are stationary when a MADF test rejects the joint null hypothesis.

For the MADF and SURADF tests, theoretically derived asymptotic null distributions are not available. The desired critical values are generated using Monte Carlo methods and are, therefore, case specific.

The third solution to the dependence problem is provided by Bai and Ng (2001a). They assume that the q_it are generated by

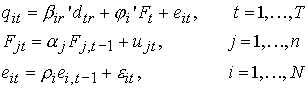(4)

where F_t is an nx1 vector of common factors, each element of which has a first-order autoregressive (AR(1)) structure and e_it is the factor specific to each series (the idiosyncratic component), also exhibiting an AR(1) structure.² The nx1 vector j_I contains the factor loadings. The setup is roughly similar to the first solution to the dependence problem where the were subtracted from each observation in a series and the panel tests were applied to the adjusted series which were expected to be less dependent. In the present case, one obtains estimates of F_t and the e_it and test for unit roots in F_t and the e_it separately so that the source of the presence or absence of a unit root in q_it may be determined. Since the estimated e_it’s are expected to be asymptotically independent, the panel procedures described in Section 2.a may be applied to these series.

Bai and Ng (2001a) describe a procedure, based on principal components, for the case of d_1t and d_2t, separately. We shall only consider the d_2t case, as that will be our principal concern in the applications. Hence, the model to be considered is the first difference of the model in (4), . It is put in mean-deviation form to yield

where, e.g., . The steps of the procedure may then be stated as follows:

i. Form the matrices

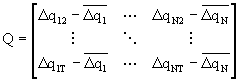and ,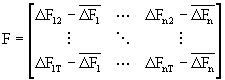

and estimate F by forming the (T-1)x(T-1) cross-product matrix QQ’ and obtaining the n eigenvectors (multiplied by (T-1)^1/2) corresponding to the first n largest eigenvalues of QQ’. The estimated loading matrix will be obtained as

ii. Set . Then, obtain and test for a unit root in each by including an intercept and trend term in the autoregressions.

iii. Set and obtain . Then, test for a unit root in each without including an intercept and trend term.

One may test for unit roots in the and the using the ADF or any other statistic that has the unit root as a null. The distributions of the ADF test when applied to the remain the same as when it is applied to the q_it. Its distribution, when applied to the , however, is now given by the distribution of the LM test of a unit root as developed by Schmidt and Lee (1991). But, note that this result is not affected by whether the are I(1) or I(0). One may also implement the panel procedures, namely, the LLC and IPS procedures, using the .

If one wishes to test the null hypothesis of stationarity, one may use the KPSS statistic to test H₀ for the with d_2t as the deterministic specification. If the are all found to be I(0), then one regresses the on a constant and time trend and applies the KPSS statistic to the residuals, , from this regression. If n* < n of the are found to be I(1), then the residuals to which the KPSS test will be applied will be obtained from the regression of on a constant, a time trend and n* of the . This residual will be denoted by . Bai and Ng (2001b) show that the KPSS statistics to test stationarity in the and have the distributions derived in Kwiatowski et al, (1992) but that the KPSS statistic to test stationarity in the has the distribution of the statistic developed by Shin (1994) for testing the null of cointegration between n* I(1) variables with a trend term included. Bai and Ng (2001b) also point out that the are asymptotically independent while the are not, so that panel procedures can only be applied to the . Thus, the Hadri approach may only be implemented if we end up obtaining the in our applications.

3. The Data

We have constructed a panel of real exchange rates with Turkey’s seventeen major trading partners: Austria, Belgium, Denmark, Finland, France, Germany, Greece, Italy, Japan, the Netherlands, Norway, Saudi Arabia, Spain, Sweden, Switzerland, the UK and the USA. The choice of trading partners was dictated by (a) the share they had in Turkey’s total trade, (b) data availability, and (c) the desire to benefit from the added heterogeneity that a larger panel may provide. We found that these seventeen countries account, on the average, for 64.5% of Turkey’s trade for the period 1989-2001. We had to leave out important trading partners such as Russia (with an average share of 5%) and Iran (1.8%) because price and/or exchange rate data were not available. On the other hand, relatively smaller trading partners, such as Denmark (0.52%), Finland (0.52%) and Greece (0.81%) were included to increase the heterogeneity in the panel.

The series are monthly and cover the period 1984.01-2001.06. The price index used in the construction of the series is the Consumer Price Index (1987=100). The exchange rates and the domestic CPI series were obtained from the Central Bank database. The foreign CPIs were downloaded from the International Financial Statistics database and their base years were shifted to 1987.

4. Empirical Results

We start by presenting the unit root tests on the individual series. The tests are the ADF and KPSS tests. The equations needed for both tests contain an intercept and a linear time trend. In this and future applications of the ADF statistic, the lag length, p_i, was chosen using three criteria: AIC, Schwartz Information Criterion (SIC) and the t-ratio for the coefficient of the last lag. A general-to-specific procedure was implemented, starting with an equation for which a large enough lag length, p_max, was specified. In all applications, p_max was chosen to be 13. Following Erlat (2002), we initially sought agreement between, at least, two of the criteria. If there was no agreement, then the result of the criterion indicating the largest lag was chosen. For this choice of p_i, autocorrelation in the residuals was tested using the Ljung-Box statistic and if significant autocorrelation was found, p_i was increased until it was eliminated.

For the KPSS statistic, the number of weights, , (see equation (3) above) was decided upon by using a procedure suggested in Mayadune et al. (1995). We took the residuals obtained from equation (2), calculated their autocorrelations and compared them with twice their standard errors, which were estimated as T^-1/2. We chose to be equal to the degree of the last significant autocorrelation.

The results of the ADF and KPSS tests are given in Table 1. We note that only for four series is the unit root null rejected in the case of the ADF tests; Italy, Norway, Sweden and the UK. The rejection for the first three is only at the 10% level while the rejection for the UK series is very strong, at 1%. On the other hand, the KPSS results indicate that the stationarity null is not rejected only for Japan, the Netherlands and the UK. The KPSS results appear to confirm the ADF results only for the UK series. They do, however, indicate stationarity for series not picked up by the ADF statistic. Given that the power of the ADF statistic is low, this may be viewed as a useful result. On the other hand, the fact that the KPSS statistic does not offer collaboration of the ADF results for Italy, Norway and Sweden is not that surprising in view of Caner and Kilian (2001) where they show that the KPSS statistic tends to reject the stationarity null more often than it should.

Table 1
ADF and KPSS Test Results
	P	ADF	LB		KPSS
Austria	2	-2.189	13.325 (0.960)	20	0.132*
Belgium	1	-2.689	16.904 (0.853)	19	0.135*
Denmark	1	-2.714	15.218 (0.914)	18	0.135*
Finland	1	-2.876	23.830 (0.471)	16	0.141*
France	1	-2.736	16.032 (0.887)	19	0.132*
Germany	1	-2.579	15.495 (0.929)	20	0.123*
Greece	1	-2.980	21.473 (0.611)	22	0.130*
Italy	1	-3.282*	21.819 (0.590)	14	0.181**
Japan	1	-2.541	17.874 (0.809)	16	0.089
Netherlands	2	-2.262	12.913 (0.968)	18	0.116
Norway	1	-3.196*	13.598 (0.955)	16	0.127*
S. Arabia	1	-2.450	10.316 (0.996)	36	0.150**
Spain	2	-2.507	16.024 (0.914)	25	0.187**
Sweden	1	-3.217*	14.607 (0.950)	22	0.174**
Switzerland	1	-2.491	15.728 (0.896)	19	0.120*
UK	1	-4.302***	27.812 (0.268)	10	0.088
USA	1	-2.856	11.263 (0.987)	27	0.153**
Notes: LB stands for the Ljung-Box statistic which has an asymptotic chi-square distribution with k-p degrees of freedom under the null, k being the number of autocorrelations. In the present case, k = 24. The figure in parentheses next to the LB statistic is its p-value. The critical values for the ADF tests are those based on MacKinnon’s (1991) response surface analysis. _p_ _T_ _0.10_ _0.05_ _0.01_ 1 208 -3.1397 -3.4324 -4.0051 2 207 -3.1398 -3.4325 -4.0053 The critical values for the KPSS tests have been obtained from Table 1 of Kwiatowski et al. (1992). _0.10_ _0.05_ _0.01_ 0.119 0.146 0.216 4. “*” : significant at the 10% level. “**” : significant at the 5% level. “***” : significant at the 1% level.

We next turn to the results of the three panel unit root tests discussed in Section 2.1, namely, LLC, IPS and Hadri. In this application of these tests the dependence between the series have not been taken into account. The results are given in Table 2. We note that both the LLC and IPS tests reject the null hypothesis of a unit root, while Hadri’s result does not corroborate

Table 2
LLC, IPS and Hadri Test Results
LLC	-2.514***
IPS	-3.390***
Hadri	6.854***
Notes: 1. All three tests are distributed as N(0, 1) asymptotically. The one-sided critical values are _0.10_ _0.05_ _0.01_ ±1.28 ±1.64 ±2.33 2. “***” : significant at the 1% level.

this outcome as the stationarity null is strongly rejected. The Hadri result appears to be consistent with the individual KPSS results of Table 1 but the same cannot be said for the LLC and IPS results. We now need to see if these results are due to the dependence between the series.

That there is a great deal of dependence between the q_it can easily be seen from their correlation matrix. However, instead of presenting this matrix, following Luintel (2001)’s lead, we simply calculated the average of the correlations to be 0.68, which is a considerably high value.

The simplest way to deal with the dependence problem was to demean the data by subtracting from each q_it. The average of the correlations between the demeaned series was now found to be 0.02, which indicates an appreciable reduction in dependence. Thus, we calculated the individual ADF tests, as well as the LLC and IPS tests using instead of q_it. The results are given in Table 3. We find that the LLC and IPS tests are no longer significant and that only two series are individually significant, at the 10% level; Netherlands and Norway. Only the Norwegian series has remained significant after demeaning.

When we apply the second solution, the MADF and SURADF tests, to the data, we find the MADF statistic to be 98.578 and its critical value, at the 10% level, to be , 121.102, so that the joint null hypothesis of a unit root is not rejected. One would expect all the individual SURADF tests to also not reject their respective unit root nulls and that is exactly what we end up with.³ They are consistent with the LLC and IPS results given in Table 3.

The final solution we implemented to deal with dependence was to partition each series into common factors and idiosyncratic components. We first tested the common factors and the

Table 3
ADF, LLC and IPS Test Results for Demeaned^1 Data
LLC		-1.196
IPS		-0.668
	p	ADF^1	LB^1
Austria	12	-2.585	6.530 (0.999)
Belgium	3	-1.804	12.731 (0.970)
Denmark	5	-2.481	22.852 (0.107)
Finland	12	-3.087	12.908 (0.968)
France	3	-1.912	13.753 (0.952)
Germany	1	-1.574	16.710 (0.861)
Greece	6	-2.141	18.863 (0.759)
Italy	3	-2.277	16.713 (0.861)
Japan	8	-3.023	14.021 (0.946)
Netherlands	12	-3.385*	5.906 (0.999)
Norway	1	-3.172*	23.029 (0.518)
S. Arabia	1	-1.429	10.589 (0.992)
Spain	1	-1.594	20.915 (0.644)
Sweden	1	-2.193	22.925 (0.524)
Switzerland	3	-2.237	23.254 (0.505)
UK	1	-2.204	31.366 (0.143)
USA	1	-1.161	23.150 (0.511)
Notes: 1. LB stands for the Ljung-Box statistic which has an asymptotic chi-square distribution with k-p degrees of freedom under the null, k being the number of autocorrelations. In the present case, k = 24. The figure in parentheses next to the LB statistic is its p-value. 2. The critical values for the ADF tests are those based on MacKinnon’s (1991) response surface analysis. _p_ _T_ _0.10_ _0.05_ _0.01_ 1 208 -3.1397 -3.4324 -4.0051 3 206 -3.1398 -3.4326 -4.0055 5 204 -3.1399 -3.4328 -4.0059 6 203 -3.1400 -3.4329 -4.0061 8 201 -3.1401 -3.4331 -4.0065 12 197 -3.1404 -3.4336 -4.0074 3. “*” : significant at the 10% level.

idiosyncratic components, separately, for unit roots and also applied the pooled tests to the idiosyncratic components.

The first question we needed to solve, however, was to choose the n common factors, F_tj. For this purpose, calculated the percentage of the total variance accounted for by the first n eigenvectors (i.e., the common factors). Since the sum of the eigenvalues is equal to the trace of the matrix [see. e.g., Srivastava (2002: 404)], then this percentage may be obtained as where l_i denotes the eigenvalues.⁴ We found that the percentage due to the first eigenvector was 86.7 and one gained only 7.3 percentage points when one considered the first three eigenvectors. Thus, we decided to choose n = 1; that is, we chose the first eigenvector as the common factor.

The ADF test results for and the idiosyncratic components are given in Table 4. We note that the null hypothesis of a unit root is not rejected for the common factor and is rejected only for the idiosyncratic component of the Japanese series. We also note, from the last two columns of Table 4, that the variation in the real exchange rates are dominated by the common factor. If all variations had been idiosyncratic, then the figures in the first of these two columns would have been close to unity and those in the second column would have been very small. But we find that the reverse holds in all cases.

We also find the null hypothesis of a unit root not being rejected when we apply the panel procedures to the . LLC yields a value of 0.676 while IPS is found to be 3.806.

Finally, to test the null hypothesis of stationarity, we found that, since the KPSS statistic for was 0.126 and that indicated that the stationarity null should be rejected at the 10% level (see the critical value in Table 1), we need to obtain the to test the stationarity in the idiosyncratic component. Of course, we cannot apply Hadri’s approach because the are not asymptotically independent. Thus, in Table 6, we present the KPSS test results as applied to the , which were obtained, as described in Section 2.b, by regressing the on an intercept, trend term and . We find that they agree exactly with the ADF results as applied to the ; namely, only the Japanese series appear to be I(0), the rest are all I(1).

Table 4
The ADF Tests on the Common Factor and the Idiosyncratic Components
	p	ADF^2	LB^1
	1	-3.120	15.358 (0.910)
Austria^3	4	-0.855	33.607 (0.092)	0.0492	3.2939
Belgium	3	-1.063	12.712 (0.971)	0.0353	4.0873
Denmark	2	-0.983	32.985 (0.104)	0.0385	4.3638
Finland	12	-2.153	12.077 (0.979)	0.0903	1.8220
France	3	-1.026	12.461 (0.974)	0.0356	4.6489
Germany	1	-1.458	18.470 (0.780)	0.0432	3.3930
Greece	12	-1.121	7.746 (0.999)	0.1475	2.0198
Italy	3	-1.569	19.607 (0.719)	0.1029	2.3565
Japan	8	-2.905**	14.233 (0.941)	0.3572	0.7126
Netherlands	1	-2.034	27.838 (0.267)	0.0460	4.4383
Norway	1	-2.118	26.257 (0.340)	0.0586	4.8370
S. Arabia	1	-0.616	7.225 (0.999)	0.3754	0.7126
Spain	1	-0.836	19.364 (0.732)	0.0765	1.9313
Sweden	1	-1.252	24.032 (0.460)	0.1266	2.3136
Switzerland	3	-2.128	23.618 (0.484)	0.1065	2.6512
UK	1	-1.296	28.805 (0.228)	0.1671	1.7602
USA	1	-0.796	16.315 (0.876)	0.3480	0.8683
Notes: 1. LB stands for the Ljung-Box statistic which has an asymptotic chi-square distribution with k-p degrees of freedom under the null, k being the number of autocorrelations. In the present case, k = 24. The figure in parentheses next to the LB statistic is its p-value. 2. The ADF statistic for usual Dickey-Fuller distribution. Hence, the critical values given below are from MacKinnon’s (1991) response surface results and are for an autoregression with an intercept and trend term. _p_ _T_ _0.10_ _0.05_ _0.01_ 1 207 -3.1398 -3.4325 -4.0053 3. The critical values for the ADF test on the idiosyncratic components are from Table 1 of Schmidt and Lee (1991) and correspond to T = 200. _0.10_ _0.05_ _0.01_ -2.34 -2.63 -3.19 4. is the ratio of the variance of the idiosyncratic component to the variance of the differenced data and is the ratio of the standard deviation of the common factor to the idiosyncratic component. 5. “**” : significant at the 5% level.

Table 5
KPSS Test Results as Applied to the
		KPSS
Austria	12	0.198***
Belgium	11	0.201***
Denmark	12	0.167**
Finland	14	0.125**
France	11	0.168**
Germany	14	0.148**
Greece	18	0.140**
Italy	23	0.157*
Japan	14	0.063
Netherlands	12	0.100*
Norway	12	0.119*
S. Arabia	37	0.159**
Spain	32	0.153**
Sweden	11	0.230***
Switzerland	11	0.120*
UK	14	0.175**
USA	14	0.290***
Notes: 1. The critical values below are obtained from Table 1 of Shin (1994). _0.10_ _0.05_ _0.01_ 0.97 0.121 0.184 2. “*” : significant at the 10% level. “**” : significant at the 5% level. “***” : significant at the 1% level.

5. Conclusions

We may list our conclusions are as follows:

1. The application of the individual ADF and KPSS tests to these 17 series indicated that there was little support of the PPP hypothesis for the period in question.

2. From the application of the three panel unit root tests to the unadjusted series, support for the PPP hypothesis was given by the LLC and IPS tests, while Hadri rejected the stationarity of the series.

3. When the data was demeaned, LLC and IPS no longer supported the PPP hypothesis.

4. Similarly, there was no support for PPP from the multivariate tests, MADF and SURADF.

5. In decomposing the series into their common factors and idiosyncratic components, we found that a single common factor was sufficient to account for the common component of the series. We found that this common component was I(1) and that it dominated the variance of each q_i, implying that it was the factor contributing to the nonrejection of the null when the univariate and one of the panel tests were directly applied to the q_it. In fact, when the univariate ADF and KPSS tests were applied to the idiosyncratic components, only one series was found to be I(0). Also, the LLC and IPS procedures applied to these components strongly rejected stationarity in the panel of series.

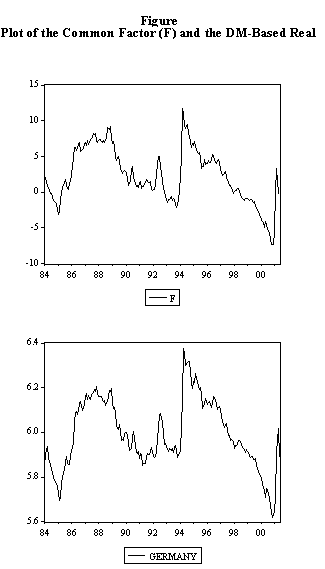
6. In sum, the support we obtained for the absolute version of the PPP hypothesis from applying the LLC and IPS procedures directly to the q_it appear to be due to ignoring the dependence between the series. The procedures where this dependence is accounted for, strongly favour the presence of a unit root in the series. A, rather informal, explanation for this outcome may be obtained from the plots of the DM-based series and the common component given in the Appendix. The majority of the series are from continental Europe and their plots are very similar to the that of the DM-based series. This strong co-movement in the series, exemplified by the common component is, apparently, not sufficiently offset by cross-sectional heterogeneity, so that the null of a unit root is not rejected when the dependence between the series is taken into account.

7. What may be done, in future research, is to incorporate structural shifts in the deterministic terms with the testing procedures. As was mentioned in the Introduction, this was done for univariate testing by Erlat (2003) and results favorable to the “quasi” PPP hypothesis were obtained.

Endnotes

1. In earlier work, restricted versions of the SUR system were used, where either the a_i were taken to be equal to a common value (Abuaf and Jorion (1990), Jorion and Sweeney (1996), O’Connell (1998)) and/or the lag length, p_i, was either set to a common non-zero value for all equations (O’Connell, 1998) or to zero (Flores et al., 1999). Higgins and Zakrajsek (2000) come closest to the models discussed above, with only the a_i restricted to be the same across equations.

2. This specification is used for simplicities sake only. In actual implementation of the procedure, higher order AR specifications may, of course, be utilized as we have done in our applications.

3. We, thus, do not present the full results here. They are available upon request.

4. Bai and Ng (2002) had developed information criteria for this purpose but they yielded good results only when both N and T were large. Since N, in our case, was rather small, we were not able to use these criteria.

References

Abuaf, N. and P. Jorion (1990): ‘Purchasing Power Parity in the Long Run’, Journal of Finance. 45(1), 157-174.

Bai, J. and S. Ng (2001a): “A PANIC Attack on Unit Roots and Cointegration”. Working Paper, Department of Economics, Boston College.

Bai, J. and S. Ng. (2001b): “A New Look at Panel Testing of Stationarity and the PPP Hypothesis’. Working Paper, Department of Economics, Boston College.

Bai, J. and S. Ng (2002): “Determining the Number of Factors in Approximate Factor Models’, Econometrica, 70(1), 191-221.

Banerjee, A., M. Marcellino and C. Osbat (2001): “Testing for PPP: Should We Use Panel Methods?”, Working Paper, Department of Economics, European University Institute.

Breuer, J.B., R. McNown and M.S. Wallace (2001): “Misleading Inferences from Panel Unit Root Tests with an Illustration from Purchasing Power Parity”, Review of International Economics, 9(3), 482-493.

Caner, M. and L. Kilian (2001): “Size Distortions of Tests of the Null Hypothesis of Stationarity: Evidence and Implications for the PPP Debate”, Journal of International Money and Finance, 20(2), 639-657.

Erlat, H. (2002): “Long Memory in Turkish Inflation Rates”, in A. Kibritcioglu, L. Rittenberg and F. Selcuk (eds.): Inflation and Disinflation in Turkey. Brookfield, Vermont: Ashgate, 97-122.

Erlat, H. (2003): “The Nature of Persistence in Turkish Real Exchange Rates”, Emerging Markets Finance and Trade, 39(2), 70-97.

Flores, R., P. Jorion, P.Y. Premont and A. Szafarz (1999): “Multivariate Unit Root Tests of the PPP Hypothesis”, Journal of Empirical Finance, 6, 335-353.

Groen, J.J. (2000): “New Multi-Country Evidence on Purchasing Power Parity: Multivariate Unit Root Test Results”, Econometric Institute Report EI 2000-9/A, Erasmus University Rotterdam.

Hadri, K. (2000): “Testing for Stationarity in Heterogeneous Panels”, Econometrics Journal, 3, 148-161.

Higgins, M. and E. Zakrajsek (2000): “Purchasing Power Parity: Three Stakes Through the Heart of The Unit Root Null”, Finance and Economics Discussion Series 2000-22, Federal Reserve Board.

Im, K.S., M.H. Pesaran and Y. Shin (2000): “Testing for Unit Roots in Heterogeneous Panels”, Working Paper, Department of Applied Economics, University of Cambridge.

Jorion, P. and R.J. Sweeney (1996): “Mean Reversion in Real Exchange Rates: Evidence and Implications for Forecasting”, Journal of International Money and Finance, 15(4), 535-550.

Kwiatowski, D., P.C.B. Phillips, P. Schmidt and Y. Shin (1992): “Testing the Null Hypothesis of Stationarity Against the Alternative of a Unit Root: How Sure Are we that Economic Time Series Have a Unit Root?”, Journal of Econometrics, 54, 159-178.

Levin, A., C.F. Lin and C.S.J. Chu (2002): “Unit Root Tests in Panel Data: Asymptotic and Finite Sample Properties”, Journal of Econometrics, 108, 1-24.

Luintel, K.B. (2001): “Heterogeneous Panel Unit Root Tests and Purchasing Power Parity”, Manchester School Supplement, 42-56.

MacKinnon, J.G. (1991): “Critical Values for Cointegration Tests” in R.G. Engle and C.W.J. Granger (eds.): Long-Run Economic Relationships. New York: Oxford University Press.

Mayadune, G., M. Evans and B. Inder (1995): “An Empirical Investigation of Shock Persistence in Economic Time Series”, Economic Record, 71, 145-156.

O’Connell, P. (1998): “The Overvaluation of Purchasing Power Parity”, Journal of International Economics, 44, 1-19.

Ozdemir, N. (2002): Panel Approaches to Testing the Persistence in Turkish Real Exchange Rates. Unpublished thesis submitted to the Department of Economics, Middle East Technical University, in partial fulfillment of the degree of Master of Science.

Sarno, L. (2000): “Real Exchange Rate Behaviour In High Inflation Countries: Empirical Evidence from Turkey”, Applied Economics Letters, 7, 285-291.

Schmidt, P. and J. Lee (1991): “A Modification of the Schmidt-Phillips Test”, Economics Letters, 36, 285-289.

Shin, Y. (1994): “A Residual Based Test for the Null of Cointegration Against the Alternative of No Cointegration”, Econometric Theory, 10(1), 91-115.

Srivastava, M.S. (2002): Methods of Multivariate Analysis. New York: John Wiley and Sons.

Taylor, M. and L. Sarno (1998): “The Behaviour of Real Exchange Rates During the Post-Bretton Woods Period”, Journal of International Economics. 46, 281-312.

Appendix