Copyright License Agreement

Presentation of the articles in the Topics in Middle Eastern and North African Economies was made possible by a limited license granted to Loyola University Chicago and Middle East Economics Association from the authors who have retained all copyrights in the articles. The articles in this volume shall be cited as follows: Erlat, G., H. Erlat, “Intra-Industry Trade and Labour Market Adjustment in Turkey”, Topics in Middle Eastern and North African Economies, electronic journal, Volume 5, Middle East Economic Association and Loyola University Chicago, September, 2003. http://www.luc.edu/publications/academic/

INTRA-INDUSTRY TRADE AND LABOUR MARKET ADJUSTMENT IN TURKEY

Guzin Erlat

Middle East Technical University

E-mail: gerlat@metu.edu.tr

Haluk Erlat

Middle East Technical University

E-mail: herlat@metu.edu.tr

Keywords: Intra-Industry Trade, Marginal Intra-Industry Trade, Smooth Adjustment Hypothesis, Panel Data

JEL Classification: F14, F16, J21, J23

Abstract: Turkey’s trade, exports in particular, expanded considerably after the major policy changes in 1980. Together with this expansion, there was also a significant increase in intra-industry trade even though the major characteristic of Turkish trade is still inter-industry. However, since intra-industry trade is hypothesised to reduce adjustment costs due to trade expansion and changes in trade patterns, this paper investigates whether this so-called “smooth adjustment hypothesis” holds for Turkey, in view of the developments in the post-1980 period.

1. Introduction

Turkey underwent important policy changes in 1980 involving trade liberalization. As a result her trade, exports in particular, expanded considerably. Together with this expansion, we also observed a significant increase in intra-industry trade (IIT); i.e., the simultaneous buying and selling of the same or similar commodities (Erlat, Erlat and Memis, 2002). Even though the dominant characteristic of Turkey’s trade was still inter-industry, the increase in IIT is very important because, on the one hand, it shows that Turkey follows the changes in world trade patterns and, on the other hand, if the expectations about the adjustment costs are lower with IIT compared to the case of inter-industry trade, then the increase in IIT will be associated with a reduction in labour costs since the reshuffling of factors of production would take place within the industry instead of between industries. But, whether this increase in IIT contributed to reductions in adjustments costs due to trade expansion is open to question and needed to be investigated.

This reduction in costs, called the “smooth-adjustment hypothesis” (SAH), is due to the fact that, movements in the labour market caused by trade expansion will take place within industries if the share of IIT is high. In fact, measures of IIT have been used to assess the degree of structural adjustment required by trade expansion. In a previous paper, (Erlat et. al, 2002), we made use of IIT measures in this sense. The measures we utilized for this purpose evaluated the share or level of IIT in new trade and are called Marginal IIT (MIIT) measures. This concept and a measure were first introduced into the literature by Hamilton and Kniest (1991). Improved measures were later developed by Brülhart (1994) and it was his C-index, which measures the level of MIIT that we used in our paper. In doing so, we operated under the simplifying assumption that changes in adjustment costs (measured as changes in employment) were exactly matched by the changes in trade flows.¹

In this paper, we undertake an econometric approach to testing the SAH. Such studies are rather limited in number. A number of them may be found in Brulhart and Hine (1999) but the majority of these studies only investigate simple correlations between employment changes and measures of IIT and MIIT. As to the econometric studies; the problem is investigated for Belgium by Tharakan and Calfat (1999), for Greece by Sarris, Papadimitriou and Mavrogiannis (1999), for Ireland by Brülhart (2000), for Malaysia by Brülhart and Thorpe (2000), and for the U.K. by Brulhart and Elliott (2002) and Greenaway, Hines and Milner (2002). Evidence in favour of the SAH are found for Ireland and Greece, but none for Belgium and Malaysia. The evidence for the U.K. are mixed. Brulhart and Elliott (2002) find evidence in favour of the SAH and, also in favour of using MIIT indexes instead of an IIT index to represent the contribution that intra-industry trade makes, while Greenaway et al. (2002: 271) conclude that there is no evidence of “… a systematic relationship between the type of trade expansion (inter- or intra-industry) and the type of employment adjustment (within or between industry adjustment) or that there is less labour market adjustment associated with intra- than inter-industry trade.”

All countries cited above are developed except Malaysia. Both because the Turkish economy is closer, in this respect, to the Malaysian economy and because we do not have access to the data on some of the variables (the proxies for the dependent variable, in particular) used by Brülhart (2000), Brülhart and Elliot (2002) and Greenaway et al. (2002) (which are the more sophisticated of the econometric applications listed above), we have applied the model in Brülhart and Thorpe (2000) to Turkish data. Thus, in the next section, we give some information about the intra-industry structure of Turkish international trade and, in doing so, also introduce the measures of IIT and MIIT that we shall utilize. In section 3, the model will be specified. The data used in the econometric application will be described in Section 4 and the empirical results will be presented. Section 5 will contain our conclusions.

2. Intra-Industry Structure of Turkish Trade

In Erlat et al (2002) we extensively investigated the IIT structure of Turkish international trade, based on 3-digit SITC (Rev. 3) data. In the present case, we needed to use an industrial classification; hence, the trade data that we shall base our analysis upon will be for 3-digit ISIC (Rev. 2) industrial sectors. They cover the period 1969-2001 and are measured in $US. They were obtained from the State Institute of Statistics (SIS) database.

We first calculated the Grubel and Lloyd (GL) (1971) index for each 3-digit industry. Letting X_it and M_it stand for the exports and imports of industry i in period t, respectively, the GL index for the ith industry at time t may be expressed as

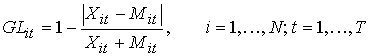(1)

GL_it lies between 0 and 1, with values close to unity indicating a high rate of IIT for the ith industry. We may aggregate the GL_it across industries by obtaining its weighted average, using the shares of each industry in total trade as the weights. The resultant expression becomes,

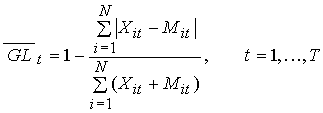(2)

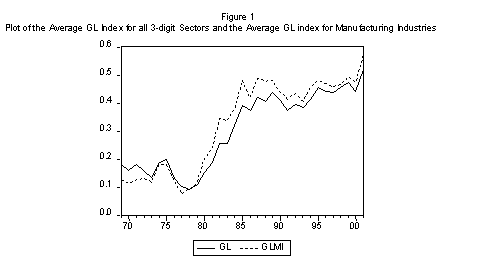
We calculated for both total trade and trade in manufactured products. The plots of both indexes are given in Figure 1. We note that the rate of IIT was low and declining prior top 1980, after which we observe a rapid increase, particularly in the manufacturing industries, until 1986, after which it slightly declines to its pre-1985 level, picking-up again after 1994. The manufacturing sector appears to be instrumental in the rise of IIT.

Let X_it and M_it, again, denote the exports and imports of industry i at period t, and let X_i,t-n and M_i,t-n be the exports and imports of i at period t-n where . Denote X_it - X_i,t-n by DX_in and M_it - M_i,t-n by DM_in.² Then, Brulhart (1994)’s A-index to measure MIIT for each industry may be expressed as,

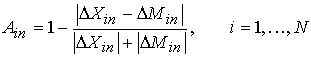(3)

and varies between 0 and 1. Values close to unity indicate that marginal trade is predominantly of the intra-industry type.

The A_in indexes may be aggregated across sectors in exactly the same way as the GL index, by obtaining their weighted average using

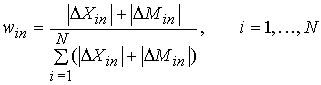
as weights. The resultant average then becomes

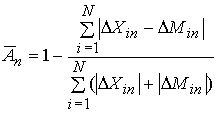(4)

We calculated this average for both total and manufacturing industry trade and for different subperiods. These subperiods were decided upon by inspecting the plots of the GL indexes given in Figure 1. The results are presented in Figure 2. There are two subperiods prior to 1980 and we note that MIIT is less than 20% in both of them; in fact, it is even lower than 5% for the 1975-1979 period. Things improve considerably after 1980. The largest jump is in the 1980-85 period. There is some decline in the next two periods. This decline is more pronounced in the MIIT component of total trade compared to that of manufacturing industry trade. However, during the last period, 1994-2001, we observe a significant increase in MIIT, particularly in manufacturing industry trade.

To sum up; the Turkish economy has exhibited considerable expansion in its international trade after 1980 and both IIT and MIIT have shown appreciable increase as a result of this expansion. The manufacturing sector appears to be the primary mover in all these developments.

3. The Model

As mentioned in the Introduction, we follow Brulhart and Thorpe (2000) and estimate the following two specifications of an equation designed to account for changes in employment in 3-digit ISIC (Rev. 2) manufacturing industries:

LDEMPL_it = b₀ + b₁ LDCONS_it + b₂ LDPROD_it + b₃ LTREX_it + b₄ IIT_it + u_it (5)

and

LDEMPL_it = b₀ + b₁ LDCONS_it + b₂ LDPROD_it + b₃ LTREX_it + b₄ IIT_it (6)

+ b₅ (IITxLTREX)_it + u_it

where u_it = m_i + e_it and e_it ~iid(0, s²). We assume the cross-section component m_i to be fixed since the 3-digit industries that make-up the panel have not been chosen at random. Hence, both specifications are estimated using a fixed effects estimator that is, basically, OLS with cross-section dummies.

The variables used may be defined as follows:

LDEMPL = The natural log of the absolute value of the change in employment (L) between t and t-n.

LDCONS = The natural log of the absolute value of the change in aparent consumption (C = Q + M - X) between t, t-n, Q being output.

LDPROD = The natural log of the absolute value of the change in labour productivity, measured as output per worker, between t and t-n.

LTREX = The natural log of trade exposure [(X+M)/Q].

IIT = May be GL, DGL or A.

IITxLTREX = The interaction between IIT and trade exposure.

LDEMPL is a proxy for the costs of adjustment in the labour market. The assumption is that the costs of moving labour across industries is proportional to the size of net changes in wage payments and, furthermore, that this proportion is the same for all industries and over time. The expected sign for the coefficient of LDCONS is positive. One would expect the coefficient of LDPROD to be negative since increases in productivity would tend to reduce the labour requirement to produce the same level of output. This expectation is supported by evidence from the accounting measure of employment change found in, e.g., Tharakan and Calfat (1999) for Belgium, Sarris et al. (1999) for Greece and Erlat (2000) for Turkey. The prior expectation for the coefficient of LTREX is that it should be positive since trade exposure is expected to increase inter-industry specialization pressures (Brulhart and Thorpe, 2000: 730). Finally, the coefficients of both IIT and IITxLTREX are expected to be negative given the smooth adjustment hypothesis. The reason for the introduction of IITxLTREX in the second specification is the expectation that IIT should matter more in sectors where the level of trade is high.

5. Empirical Results

The data used to measure the variables defined above were all obtained from the SIS database. The non-trade data are based on their annual Census of Industrial Production. This data was only available for the period 1974-1999; hence, we considered it in the estimations. This, however, is not an important shortcoming since the rate of IIT starts reaching meaningful levels after 1980. All data have been deflated using the 1987-based WPI.

We used three proxies for the IIT variable. These are, the A-index for MIIT, the change in the GL index, DGL, and the GL index itself. The A index and DGL have been calculated as yearly changes. It has been shown by Oliveras and Terra (1997) that A-indexes calculated for subintervals of a given interval cannot be aggregated to the A index for the parent interval unless the net balance of trade changes has the same sign in all subintervals. Since this situation may be the exception rather than the rule, choice of interval in calculating the A index is important. Brulhart (1999) has investigated this question within the context of testing the SAH and has reached the conclusion that A indexes based on yearly changes give the best results.³

The estimates are given in Table 1. We find that (a) the coefficient of IIT is positive in all specifications and for all proxies except for the coefficient of GLxLTREX; this estimate, however, is not statistically significant, (b) the coefficient of the A-index, even though positive, is statistically significant in the specification with the interaction term and so is the coefficient of the interaction term, (c) the coefficients of DGL and DGLxLTREX are positive but statistically insignificant, while the coefficient of GL in the model without an interaction term is positive and significant, but becomes insignificant when GLxLTREX is introduced. These results are the reverse of what is expected when testing the SAH and appear to be closer to what Brulhart and Thorpe (2000) found for Malaysia. They call their findings for Malaysia “puzzling” but, in view of Tharakan and Calfat (1999) and Greenaway et al. (2002)’s

Table 1
Panel Data Estimates For Yearly Changes
	(1)		(2)		(3)
	No interaction	Interaction	No interaction	Interaction	No interaction	Interaction
LDCONS	0.219 (5.236)^c1	0.225 (5.379)^c	0.224 (5.346)^c	0.224 (5.345)^c	0.212 (5.038)^c	0.212 (5.043)^c
LDPROD	-0.024 (-0.577)	-0.020 (-0.490)	-0.024 (-0.569)	-0.024 (-0.566)	-0.035 (-0.841)	-0.036 (-0.845)
LTREX	0.172 (2.366)^b	0.099 (1.259)	0.178 (2.454)^b	0.178 (2.437)^b	0.149 (2.034)^b	0.168 (1.757)^a
A	0.228 (1.403)	0.626 (2.686)^c	-	-	-	-
AxLTREX	-	0.320 (2.374)^b	-	-	-	-
DGL	-	-	0.262 (1.043)	0.312 (0.737)	-	-
DGLxLTREX	-	-	-	0.019 (0.145)	-	-
GL	-	-	-	-	0.492 (2.322)^b	0.417 (1.283)
GLxLTREX	-	-	-	-	-	-0.041 (-0.306)
R^2	0.3631	0.3682	0.3623	0.3623	0.3662	0.3663
F	131.499^c	100.695^c	131.041^c	98.147^c	133.287^c	99.858^c
SSR^2	1099.996	1091.093	1101.391	1101.357	1094.593	1094.445
DW	1.836	1.832	1.829	1.829	1.833	1.833
FE Test^3	6.752^c	6.779^c	6.777^c	6.677^c	6.824^c	6.817^c
Chow Test^4	3.236^b	2.137^a	2.595^b	2.756^b	2.318^a	2.030^a
NT	725	725	725	725	725	725
Notes: The figures in parentheses are t-ratios. SSR stands for the sum of squared residuals. “FE Test” stands for the test of whether the fixed effects are statistically significant. It will have an F-distribution with 28 and 725-29-k degrees of freedom, where k is the number of regressors besides the dummy variables representing the fixed effects. “Chow Test” stands for the test of whether there has been a structural shift between the (1974-75)-(1979-80) period and the (1980-81)-(1998-99) period, regarding the k non-dummy regressors. (^a) : Significant at the 10% level, (^b) : Significant at the 5% level, (^c) : Significant at the 1% level.

empirical results and Lovely and Nelson (2000, 2002)’s theoretical predictions, neither their findings, nor ours may be unexpected. In fact, Lovely and Nelson (2000) construct a model where the change in total trade is all intra-industry but labour adjustment is all inter-industry. Thus, our expectations regarding the sign of the coefficient of A need not be so strong.

The coefficient of LDCONs is positive in all cases and they are all statistically significant. On the other hand, the coefficient of LDPROD is negative in all cases but they are all statistically insignificant. Finally, the coefficient of the trade exposure variable, LTREX, is positive in all cases and is statistically significant except in the specification with an interactive term and the A-index used as a proxy for IIT.

We also performed two sets of tests for both specifications. The first is a test of whether the fixed effects specification is valid. We find this specification to hold in all cases. The second test, the Chow test, is used to test if the coefficients of the regressors, LDCONS, LDPROD, LTREX, IIT and IITxLTREX, are the same for the subperiods (1974-75)-(1979-80) and (1980-81)-(1998-99). The outcomes of the test, in all cases, indicate that a statistically significant structural shift has occurred after 1980. This shift, apparently, is due to a significant shift in the coefficient of LDPROD, turning it from a positive value to a negative one.⁴

We also considered subsets of the manufacturing industries that exhibited high IIT and MIIT rates. To determine these subsets we first calculated the means of the GL_it and A_it over the period 1980-2001 and then took the average of these means across industries. Industries with time-wise means greater than these averages were chosen. The industries in question are given in Table 2. The first column has the industries with high IIT rates, while the second column has the industries with high MIIT rates. The final column contains the industries with both high IIT and MIIT rates. We note that the intersection of the high IIT industry set and the high MIIT industry set is not very large, implying that the correlation between the GL and A indexes is relatively low.

We estimated the two specifications given in equations (5) and (6) for all three subsets using yearly changes. The results are presented in Table 4. and contain only the coefficient estimates of the three IIT proxies, A, DGL and GL. The coefficient of LDCONS is positive and significant, while the coefficient of LDPROD is negative and insignificant in all cases considered. The coefficient of LTREX is also positive throughout but its statistical significance varies.⁵

We note that we now have a few negative coefficient estimates but only one of these, the coefficient of GLxLTREX for the subset with high MIIT rates, is significantly different from zero, but only at the 10% level of significance. It is hard to

Table 2
Industries with High IIT and/or MIIT Rates
(a)	(b)	(c)
311 Food manufacturing	311 Food manufacturing	311 Food manufacturing
314 Tobacco manufactures	313 Beverage industries	314 Tobacco manufactures
323 Manufacture of leather and products of leather, leather substitutes and fur, except footwear and wearing apparel	314 Tobacco manufactures	323 Manufacture of leather and products of leather, leather substitutes and fur, except footwear and wearing apparel
324 Manufacture of footwear, except vulcanized or molded rubber or plastic footwear	321 Manufacture of textiles	324 Manufacture of footwear, except vulcanized or molded rubber or plastic footwear
331 Manufacture of wood and wood and cork products, except furniture	323 Manufacture of leather and products of leather, leather substitutes and fur, except footwear and wearing apparel	356 Manufacture of plastic products not elsewhere classified
332 Manufacture of furniture and fixtures, except primarily of metal	324 Manufacture of footwear, except vulcanized or molded rubber or plastic footwear	371 Iron and steel basic industries
353 Petroleum refineries	341 Manufacture of paper and paper products	372 Non-ferrous metal basic industries
356 Manufacture of plastic products not elsewhere classified	342 Printing, publishing and allied industries	381 Manufacture of fabricated metal products, except machinery and equipment
361 Manufacture of pottery, china and earthenware	351 Manufacture of industrial chemicals	390 Other Manufacturing Industries
369 Manufacture of other non-metallic mineral products	352 Manufacture of other chemical products
371 Iron and steel basic industries	356 Manufacture of plastic products not elsewhere classified
372 Non-ferrous metal basic industries	362 Manufacture of glass and glass products
381 Manufacture of fabricated metal products, except machinery and equipment	371 Iron and steel basic industries
390 Other Manufacturing Industries	372 Non-ferrous metal basic industries
	381 Manufacture of fabricated metal products, except machinery and equipment
	382 Manufacture of machinery except electrical
	383 Manufacture of electrical machinery apparatus, appliances and supplies
	390 Other Manufacturing Industries

claim that this constitutes evidence in favour of the smooth adjustment hypothesis. The rest of the coefficient estimates are again positive and the strongest results are found for the high MIIT subset but for the coefficients of DGL and GL, not, as one would expect, for the coefficient of A.

5. Conclusions

In this paper, we sought to test the smooth adjustment hypothesis based on an

Table 3
Panel Data Estimates for Subgroups of Industries Based on Yearly Changes
	(a)		(b)		(c)
	No interaction	Interaction	No interaction	Interaction	No interaction	Interaction
A^1	0.217 (1.015)^2	0.667 (1.859)^a	0.185 (0.954)	0.408 (1.392)	0.275 (1.018)	0.652 (1.295)
AxTREX	-	0.344 (1.561)	-	0.192 (1.014)	-	0.368 (0.886)
DGL	-0.112 (-0.370)	0.679 (1.279)	0.917 (2.452)^b	0.126 (0.201)	0.708 (1.457)	-0.108 (-0.106)
DGLxTREX	-	0.405 (1.815)^a	-	-0.436 (-1.566)	0.708 (1.457)	-0.671 (-0.910)
GL	0.306 (1.241)	0.811 (1.929)^a	0.710 (2.421)^b	-0.0003 (-0.0005)	0.591 (1.607)	0.865 (1.136)
GLxTREX	-	0.338 (1.481)	-	-0.469 (-1.890)^a	-	0.214 (0.410)
N	15	15	18	18	9	9
T	25	25	25	25	25	25
NT	375	375	450	450	225	225
Notes: 1. The estimates are obtained from models that contain, in addition to the IIT proxies, LDCONS, LDPROD and LTREX as explanatory variables. The estimates pertaining to their coefficients are not presented in order to focus on the IIT proxies. 2. The figures in parentheses are t ratios. 3. (^a) : Significant at the 10% level, (^b) : Significant at the 5% level, (^c) : Significant at the 1% level.

econometric model previously estimated by Brulhart and Thorpe (2000) for Malaysia. We used panel data based on the ISIC (Rev.2) classification. We may list our conclusions as follows:

1. We considered the period (1974-75)-(1998-99) and found, when all manufacturing industries were considered, that the coefficients of the IIT proxies were all positive except for one (GLxLTREX) which was, nevertheless, statistically insignificant. Although this result appears to go against expectation, whether this expectation is always warranted is open to question. All IIT proxies, A included, are production based measures. But, as Lovely and Nelson (2002: 192) argue, “... changes in trade patterns reflect changes in production and demand.” Hence, the expected sign of the changes in employment due to IIT may not, necessarily, be negative.

2. Coefficients that were positive and statistically significant were obtained using the A and GL indexes, but not DGL.

3. We also repeated the estimations for subsets of the industries with high IIT and/or MIIT rates. In this case, we were able to obtain more significant results but only one of these were negative. We also noted that now both DGL and GL appeared to indicate stronger relationships with changes in employment.

4. In sum, we were able to obtain some evidence of a significant relationship between employment changes and IIT but, if we adhered to the strict expectation that such a relationship should be negative, then we would have to agree with Brulhart and Thorpe (2000) that this evidence is “puzzling”. But there are both empirical and theoretical grounds for us to not entertain such a strict prior.

Endnotes

1. Brulhart (1999) contains a simplified model where this holds. The link between MIIT and adjustment costs is also discussed theoretically by Azhar, Elliot and Milner (1998) and Lovely and Nelson (2000, 2002).

2. The X and M’s are now measured in real terms since the MIIT indexes measure real changes in trade flows. We, thus, expressed all series in TL terms using period-average exchange rate series and, subsequently, adjusted them for inflation using the 1987 based Wholesale Price Index (WPI). The exchange rate and WPI series were obtained from the Central Bank database.

3. A indexes based on yearly changes would show a lot of volatility; so we also carried out our estimations using three-yearly changes which are expected to show a smoother picture. The outcomes of these estimations did not lead to any changes in our conclusions. Hence, we are not presenting them here. They are available upon request.

4. The estimates of the model with structural shift dummies are available upon request. We also estimated the two models for the (1980-81)-(1998-99) subperiod. The results were similar to the ones obtained for the full period and are not repeated here. They, also, are available upon request.

5. The detailed estimation results are available upon request.

References

Azhar, A.K.M., R.J.R. Elliot and R.C. Milner (1998): “Static and Dynamic Measurement of Intra-Industry Trade and Adjustment: A Geometric Appraisal”, Weltwirtschaftliches Archiv, 134, 404-422.

Brulhart, M. (1994): “Marginal Intra-Industry Trade: Measurement and Relevance for the Pattern of Industrial Adjustment”, Weltwirtschaftliches Archiv, 130, 600-613.

Brulhart, M. (1999): “Marginal Intra-Industry Trade and Trade-Induced Adjustment: A Survey” in M. Brulhart and R.C. Hine (eds.): Intra-Industry Trade and Adjustment: The European Experience. London: Macmillan Press, 36-69.

Brulhart, M. (2000): “Dynamics of Intra-Industry Trade and Labour Market Adjustment”, Review of International Economics, 8, 420-435.

Brulhart, M. and R.J.R. Elliott (2002): “Labour Market Effects of Intra-Industry Trade: Evidence for the United Kingdom”, Weltwirtschaftliches Archiv, 138, 207-228.

M. Brulhart and R.C. Hine (eds.) (1999): Intra-Industry Trade and Adjustment: The European Experience. London: Macmillan Press.

Brulhart, M. and M. Thorpe (2000): “Intra-Industry Trade and Adjustment in Malaysia: Puzzling Evidence”, Applied Economics Letters, 7, 729-733.

Erlat, G. (2000): “Measuring the Impact of Trade Flows on Employment in the Turkish Manufacturing Industry”, Applied Economics, 32, 1169-1180.

Erlat, G., H. Erlat and E. Memis (2002): “Measuring Intra-Industry and Marginal Intra-Industry Trade: The Case for Turkey”, Working Paper, Department of Economics, Middle East Technical University.

Greenaway, D., M. Haynes and C. Milner (2002): “Adjustment, Employment Characteristics and Intra-Industry Trade”, Weltwirtschaftliches Archiv, 138, 254-276.

Grubel, H. and P.J. Lloyd (1971): “The Empirical Measurement of Intra-Industry Trade”, Economic Record, 470, 494-517.

Hamilton, C. and P. Kniest (1991): “Trade Liberalization, Structural Adjustment and Intra-Industry Trade”, Weltwirtschaftliches Archiv, 127, 356-367.

Lovely, M.E. and D.R. Nelson (2000): “Marginal Intra-Industry Trade and Labour Adjustment”, Review of International Economics, 8, 436-477.

Lovely, M.E. and D.R. Nelson (2002): “Intra-Industry Trade as an Indicator of Labour Market Adjustment”, Weltwirtschaftliches Archiv, 138, 179-206.

Oliveras, J. and I. Terra (1997): “Marginal Intra-Industry Trade Index: The Period and Aggregation Choice”, Weltwirtschaftliches Archiv, 133, 170-179.

Sarris, A.H., P. Papadimitriou and A. Mavrogiannis (1999): “Greece” in M. Brulhart and R.C. Hine (eds.): Intra-Industry Trade and Adjustment: The European Experience. London: Macmillan Press, 168-187.

Tharakan, P.K.M., and G. Calfat (1999): “Belgium” in M. Brulhart and R.C. Hine (eds.): Intra-Industry Trade and Adjustment: The European Experience. London: Macmillan Press, 121-134.