Abdel-Hameed M. Bashir*, Department of Economics, Grambling State University, E-mail: Bashirah@alpha0.gram.edu

The rapid growth of foreign direct investment (FDI) and its overall magnitude had sparked numerous studies dealing with the channels of transmission from FDI to growth. Theoretically, models of "endogenous" growth were recently combined with studies on the diffusion of technology in an attempt to emphasize the major role played by FDI in the economy [see Barro (1990), Lucas (1988)]. In these models, technology plays a fundamental role in the process of economic development. Moreover, the extensions of the neoclassical models to allow for international mobility of capital and technology have reinforced the notion that low-income countries tend to grow at higher rates [see Barro (1991)]. The new developments have also indicated the volatility of FDI and called for important macroeconomic and financial adjustments¹. Meanwhile, the original contribution of these models is that, financial liberalization and stabilization must be undertaken by host countries before any increases in FDI become feasible (see De Gregorio and Guidotti, 1995).

The purpose of this paper is to examine the empirical relationship between FDI and per capita GDP growth in selected MENA countries for the years 1975-1990. To our knowledge, no attempts have so far been made to investigate the relationship between FDI and economic growth in the selected countries². In particular, the paper aims to construct an endogenous growth model in which the rate of technological progress is the primary determinant of GDP growth rate. The theoretical model will then be empirically tested to examine the effects of FDI on economic growth. The rest of the paper is organized as follows. In section 2 we construct a growth model in which production depends on an exogenous state of technology, human and physical capital. The key to our model is that there is a fixed amount of human capital, but different types of capital goods produced by both domestic and foreign firms. We show that the larger the number of foreign firms (MNCs) operating in the economy, and the higher the level of human capital, the higher the growth rate of the economy. In section 3, we substantiate the above-explained findings empirically using panel data. The results are qualified and interpreted in the light of the recent developments in the theory of economic growth. Finally, section 4 provides some concluding remarks.

Using Spence (1976) and Ethier (1982), and closely following Barro and Sala-i-Martin (1995), suppose that the production function is given by

(1) Y = A H^{(1- a )} å _j^N₌₁ ( k_j )a

Where 0<a < 1, Y is the aggregate output, H is the stock of human capital in the economy, k_j is the capital good used by the jth firm, and A is a fixed technology parameter. There are N firms engaged in the production process, n domestic firms, and N-n foreign firms (MNC). Technological progress takes the form of expansion in N, the number of firms undertaking production. It can easily be shown that if the units of capital are all employed in the same quantities across firms, i.e., k_j = k_j+1 = K, then equation (1) can be written as:

(2) Y = A H^{(1-a )} (NK)a N^1-a

Equation (2) indicates that production exhibits constant returns to scale in H and NK. The technological progress is captured by the fact that, for given quantities of H and NK, the term N^{(1-a )} indicates that output increases with N. Assume that the price of the capital good is P_j the price of H is normalized to one, and the producers operate in a competitive market. Since the producers take these prices as given, then profit maximization entails equating the price P_j to marginal productivity of capital. Solving for the optimal amount of capital employed by firm j:

(3)K_j = H (a A/P_j)^{1/ (1-a )}

Equation (3) shows the quantity demanded of K_j depends only on the price P_j.

Suppose that each time the firm engages in production, it incurs one unit of output to use K_j. Then the present value of future cash flows for the jth firm is

(4) V(t) = å _j^N₌₁ (P_j-1) K_j e^{- rt}

Where, r is the steady state rate of return of capital. Equation (4) shows that the cost of production can be covered only if the sales price, P_j , exceeds the marginal cost of production, 1, (i.e., P_j >1). Borensztein, De Gregorio and Lee (1995) assumed that the process of adaptation of new technology of production requires a set up cost j (N-n, N/N^*). This cost is inversely related to the number of foreign firms (MNC), and to the ratio of the number of goods produced in the domestic (developing) economy to the number of goods produced in foreign (developed) economy. Now the profit of the jth firm is P _j (t) = V(t) - j (N-n, N/N^*). The competitive firm will choose the quantity K_j to maximize P _j (t), where K_j is given by equation (3). In fact equation (3) indicates that the choice variable is P_j , and the expression to maximize is (P_j -1) H . (a A/P_j)^{1/(1-a )}.

The optimal solution to the maximization problem is

(5) P_j = P = 1/a >1

Hence, the price P_j is constant over time and is the same for all capital goods j. The cost of production is also the same for all goods and each good enters symmetrically into the production function (see Barro and Sala-i-Martin, 1995, Chap. 6). Substituting equation (5) into equation (3) will determine the aggregate quantity produced of each capital good:

(6) K_j = K = H (Aa ²)^{1/ (1-a )}

The quantity K_j is the same for all goods at all points in time (if H is constant). If we substitute for P_j and K_j into equation (4), expression for the net present value is now:

(7) V(t) = H A^{1/(1-a )} (1-a )/a . a ^{2/ (1-a )} . å _j^N e^-r(v-t)

Assuming free entry in the product market, equilibrium will indicate that

(8) j = H A^{1/(1-a )} (1-a )/a . a ^{2/ (1-a )} . å _j^N e^-r(v-t)

As the number N gets large, the summation reduces to 1/r and hence, the zero-profit condition V(t) = n implies

(9) r = (H/j ) A^{1/(1-a )} (1-a )/a . a ^{2/ (1-a )}

That is, the rate of return, r, is pegged by the underlying technology and the marginal productivity of capital.

We further assume that the households are represented by the standard, infinitely-lived, Ramsey consumer who maximizes the utility function:

(10) U = å _t^¥ (C^q - 1)/(1-q ) . e^{-r t}

where C is consumption, r is the subjective rate of time preference, and q is the inverse of the intertemporal elasticity of substitution. Households earn the rate of return on asset and the wage rate w (normalized to 1) on the fixed quantity H of human capital. The key condition characterizing the solution for utility maximization will reveal the growth rate:

(11) g _c = (1/q ). (r - r )

Equation (11) indicates that, in steady-state equilibrium, the rate of growth of consumption is positively associated with the rate of return, and negatively related to the rate of time preference and the elasticity of substitution. Moreover, the number of firms, N, and the level of output, Y, will grow at the same rate of growth of consumption g _c.

Substituting equation (9) into equation (11), we get the following expression for the rate of growth of the economy:

(12) g = (1/q ) {(H/j ) . A^{1/(1-a )} (1-a )/a . a ^{2/ (1-a )} - r }

The expression in (12) is valid only if the parameters are such that g ³ 0.

Equation (12) then shows that the rate of growth of the economy is solely determined by the household's preference parameters, r, and q , and the level of technology, A. A reasonable interpretation of equation (12) is that, a greater willingness to save - lower r and q - and a better technology - higher A - will raise the rate of growth of the economy. Alternatively, a decrease in the set up cost j (an increase in the number of MNC) will raise the rate of return and raise the rate of grow g . Equation (12) also shows that, a high level of human capital, H, raises the rate of growth, g . Therefore both factors, more MNC and higher H, have positive impacts on the rate of growth of the economy³.

The degree of association between FDI and economic growth will be tested using data from a sample of six MENA countries during the period 1975-90. The countries in the sample are chosen on data availability basis. The econometric technique employed can be discussed briefly by writing the equation (12) above in the linear form:

(13) g _it = a _i + b ₁ FDI_it + b ₂ H_it + b ₃ (FDI*H)_it + b ₄ X_it + u_it

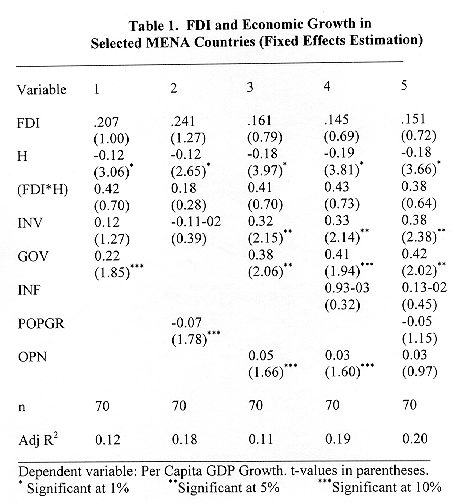
Where, i denote a country and t a time-period. a _i is a country-specific parameter. g _it represents the rate of growth of per capita GDP adjusted for the terms of trade, while X_it is a matrix of other growth determinants. A key issue in the use of panel data is how the country-specific effect is treated and consequently how the parameters should be estimated. There are two ways of estimating equation (13) using panel data: the "fixed effects" method which includes a dummy variable and uses OLS, and the "random effects" method which considers the a _i as a random variable, and therefore, uses generalized least squares (GLS). Both procedures provide consistent estimates. The main results are provided in table (1), for the fixed effects method, and table (2), for the random-effects method. Regression (1) in table 1 indicates that the correlation between growth and FDI is positive. Although the result confirms the theoretical findings established in section II above, the coefficient is not statistically significant. This certainly contradicts previous studies, which showed a strong and positive correlation between growth and foreign investment [see De Gregorio (1992)]. The variable representing human capital (H), is negatively correlated with growth, contradicting theoretical findings. While the interaction variable (FDI*H) is positive, it is not statistically significant. In regression 2, FDI has a positive impact on growth while H has a negative and statistically significant effect. Population growth (POPGR) also seems to impact growth negatively. Regressions, 3, 4, and 5 in table (1), add relevant variables such as openness to international trade (OPN), and inflation (INF), and drop some of those in regressions 1 and 2. Openness (OPN) is positively correlated with GDP growth, and statistically significant at the 10% level.

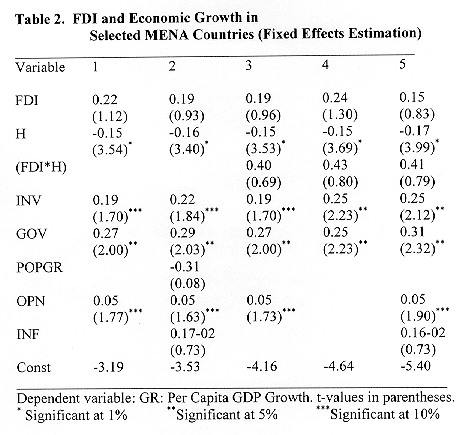
Table (2) contains the 'random effects' method estimates. In all the regressions, the coefficient of FDI is positive but not significantly different from zero. This result should not be surprising since all countries in the sample had received insignificant amount of foreign direct investment during the 1970s and 1980s. In fact they experienced hardship in getting foreign loans. The proxy of human capital is still negative but statistically significant in all versions of the growth regressions. Again this result is expected since all countries in the sample were experiencing lower secondary school enrollment ratios during the study period. Previous studies (Barro, 1991) found a positive and significant effect of the secondary school enrollment rate, when used as a proxy for human capital. When the primary school enrollment rate was used as a proxy for investment in human capital, the coefficient is significant. Moreover, the positive and statistically significant effect of government spending (GOV) contradicts the crowding-out effect predicted by the neoclassical growth model. This is an indication that the governments in these countries still play a leading role in the development process. Indeed, part of the government spending in these countries was used to build infrastructure and institutions to attract foreign investment. Finally, the regression equations in table (1) performed slightly better than those in table (2).

This paper has examined the relationship between foreign direct investment and economic growth theoretically and empirically. The review of the literature and our findings suggest that, by and large, foreign direct investment leads to economic growth. The effect, however, varies across regions and over time. Our results also indicate that domestic investment and openness to international trade are complementary to economic growth. More comprehensive studies are very much needed in this area.

³Note that the number of foreign firms (N-n) affects j , the cost of adaptation of technology negatively.

Barro, R., " Government Spending in a Simple Model of Endogenous Growth," Journal of Political Economy, Vol. 98, No. 5 (1990) pp. S103-S125.

_______, "Economic Growth in a Cross Section of Countries," Quarterly Journal of Economics, Vol. CVI, No. 2 (1991) pp. 407-444.

_______ and Sala-i-Martin, Economic Growth, Mc Grow-Hill, 1995, Chap. 5.

Barro, R., Mankiw, G., and Sala-i-Martin, X., "Capital Mobility in Neoclassical Models

of Growth," American Economic Review, Vol. 85, No. 1 (1995) pp. 103-115.

Borensztein, E. , J. De Gregorio, and J. W. Lee, "How Does Foreign Direct Investment Affects Economic Growth?," Working Paper No. 5057, Cambridge, MA:

National Bureau of Economic Research (1995).

De Gregrio, J. , "Economic Growth in Latin America," Journal of Development Economics, Vol. 39 (1992) pp. 59-84.

_______ and P. Guidotti, "Financial Development and Economic Growth," World Development, Vol. 23, No. 3 (1995) pp. 433-448.

Greene, W. H., Econometric Analysis, Third Edition, Prentice Hall (1997), Chapter 14.

International Monetary Fund, International Financial Statistics Yearbook, 1994.

Summers, R., and A. Heston, "The Penn World Table (Mark 5): An International Comparisons, 1950-1988," The Quarterly Journal of Economics, Vol. CVI, No. 2 (1991), pp. 327-368.

Back to Volume 1

Back to Topics in Middle Eastern and North African Economies Journal Home Page